Tech Design.....
___________________________
Active equalization methods for 1st order gradient woofer systems
(dipole and cardioid).
___________________________
Active equalization methods for 1st order gradient woofer systems
(dipole and cardioid).
It is well known that the on axis response of1st order gradient woofer systems, dipole and cardioid
woofers, rolls off at 6dB/octave below the dipole pole peak. The frequency of the peak is given as
Fp = c/2D
for a dipole and as
Fp = c/4D
for a cardioid where D is the effective separation of the sources and C is the speed of sound. An
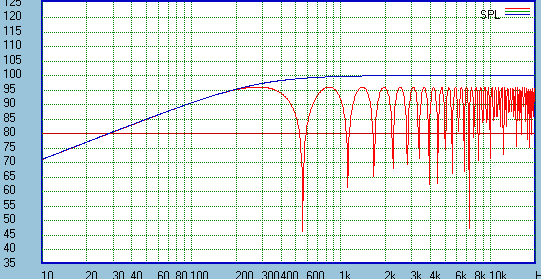
example of the response curve for a dipole composed of two ideal monopole sources separated by 2
feet is shown in Figure 1 in red.
woofers, rolls off at 6dB/octave below the dipole pole peak. The frequency of the peak is given as
Fp = c/2D
for a dipole and as
Fp = c/4D
for a cardioid where D is the effective separation of the sources and C is the speed of sound. An
example of the response curve for a dipole composed of two ideal monopole sources separated by 2
feet is shown in Figure 1 in red.
This transfer function can be factored for Qts < 0.5 as the product of two 1st order, high pass
responces:
responces:
with s1 = jF/F1 and s2 = jF/F2, where F1 and F2 are related to the "poles" of T(s), s = jF/sqrt(F1 x
F2) and Qts = Sqrt(F1 x F2) / (F1 + F2). In general, F1 < Fs and F2 > Fs. As Qts approaches 0.5 or
Qtc, F1 and F2 approach Fs.
We should also note that a 2nd order high pass response with Qts > 0.5 can be expressed as the
product of a critically damped (Qc = 0.5) response and Q boost filter with gain, G = Qts/Qc:
F2) and Qts = Sqrt(F1 x F2) / (F1 + F2). In general, F1 < Fs and F2 > Fs. As Qts approaches 0.5 or
Qtc, F1 and F2 approach Fs.
We should also note that a 2nd order high pass response with Qts > 0.5 can be expressed as the
product of a critically damped (Qc = 0.5) response and Q boost filter with gain, G = Qts/Qc:
The response 1/2 octave below the dipole peak follows that of a 1st order high pass filter with 10dB
gain, as shown in blue, and is given by the 1st order, high pass transfer function,
gain, as shown in blue, and is given by the 1st order, high pass transfer function,
Here s is the normalized, complex frequency, s = jF/Fp.Thus, to obtain flat response the woofer
system must be equalized, or the response boosted at low frequency, to compensate for this roll off.
Here are presented several methods of developing active equalization circuits for 1st order gradient
woofer systems. First are presented methods for woofers with free air Qts less than 0.5. Then methord
for woofer with Qts greater than 0.5 are presented.
Before discussing the methods of equalization it is useful to review the basic response characteristics
of a woofer in an infinite baffle. At low frequency the acoustic response of the woofer has a transfer
function which is that of a 2nd order high pass filter:
system must be equalized, or the response boosted at low frequency, to compensate for this roll off.
Here are presented several methods of developing active equalization circuits for 1st order gradient
woofer systems. First are presented methods for woofers with free air Qts less than 0.5. Then methord
for woofer with Qts greater than 0.5 are presented.
Before discussing the methods of equalization it is useful to review the basic response characteristics
of a woofer in an infinite baffle. At low frequency the acoustic response of the woofer has a transfer
function which is that of a 2nd order high pass filter:
The unequalized, on axis response of a gradient woofer system, below the on axis peak, can be
expressed as a combination of three 1st order high pass responses when the driver has Qts less
than 0.5:
expressed as a combination of three 1st order high pass responses when the driver has Qts less
than 0.5:
To equalize this response to a desired cut off frequency, Fc and Q the following steps can be applied:
1) shift the pole of the first term in the response from F1 to Fc,
2) shift the pole of the second term of the response from F2 to Fc,
3) apply equalization which is the inverse of the last term in the response.
These three steps will yield an equalized response with Q = 0.5 = Qc, and cut off frequency Fc. To
further increase Q to a desired Qd greater than 0.5,
4) apply a Q boost filter with gain, G = Qd/Qc = 2 Qd.
There is one caveat with this approach. The inverses equalization of step 3 requires infinite gain at
DC. This, in effect shifts, the pole of the roll off from the on axis peak to 0 Hz. As this is impractical,
this equalization terms is usually limited to shifting the pole of the roll off to some acceptable low
frequency. For low Q woofers where F1 is significantly below the desired cut off frequency limiting
the equalization to F1 is a suitable choice. However, if F1 is relatively close to the desired cut off
frequency then this equalization should be curtailed no sooner that one octave below the cut off
frequency. In the case where F1 is well below the cut off frequency, curtailing this equalization at F1
actually simplifies the equalization process as. Figure 2 below shows the effect of limiting the
equalization for a case where the on axis peak is be at 268 Hz and the equalization is curtailed at 16
Hz. This would be suitable for a system with Fc = 32 Hz, for example.
1) shift the pole of the first term in the response from F1 to Fc,
2) shift the pole of the second term of the response from F2 to Fc,
3) apply equalization which is the inverse of the last term in the response.
These three steps will yield an equalized response with Q = 0.5 = Qc, and cut off frequency Fc. To
further increase Q to a desired Qd greater than 0.5,
4) apply a Q boost filter with gain, G = Qd/Qc = 2 Qd.
There is one caveat with this approach. The inverses equalization of step 3 requires infinite gain at
DC. This, in effect shifts, the pole of the roll off from the on axis peak to 0 Hz. As this is impractical,
this equalization terms is usually limited to shifting the pole of the roll off to some acceptable low
frequency. For low Q woofers where F1 is significantly below the desired cut off frequency limiting
the equalization to F1 is a suitable choice. However, if F1 is relatively close to the desired cut off
frequency then this equalization should be curtailed no sooner that one octave below the cut off
frequency. In the case where F1 is well below the cut off frequency, curtailing this equalization at F1
actually simplifies the equalization process as. Figure 2 below shows the effect of limiting the
equalization for a case where the on axis peak is be at 268 Hz and the equalization is curtailed at 16
Hz. This would be suitable for a system with Fc = 32 Hz, for example.

I present this rather imposing equation not to intimidate you but rather to show just how simple the
required equalization really is. Let us examine the equation term by term. The first two terms shift the
drivers poles to achieve a Q = 0.5 response at Fc and are recognized as 1st order shelving functions
with gains, G1 = F1/Fc, and G2 = F2/Fc. (Note that G1 < 1.0 and G2 > 1.0 if F1< Fc< F2.) The third
term is the gradient equalization which is also a shelving function with gain, Gst = Fp/Fst where Fst is
the frequency where the equalization is stopped. The center frequencies of the shelving filters are
given as sqrt(F1 x Fc), sqrt(F2 x Fc), and sqrt(Fp x Fst). The fourth term is a Q boost filter with gain,
Gd = Qd/ Qc and center frequency Fc, introduced to raise the response Q from Qc = 0.5 to the
desired Qd. The last term is a simple attenuation by 10 dB. Terms 1, 2 and 4 could be replaced by a
Linkwitz transformation if suitable. However, if the desired woofer target response is for Q = 0.5, term
4 is omitted and as to be shown, terms 1 and 3 can be combined into a single shelving function
making the equalization a simple combination of two shelving functions.
It was previously stated that if the woofer was low Q with F1 well below (an octave or more) the
desired cut off frequency then the gradient equalization could be curtailed at F1 yielding a
simplification in the equalization transfer function. To see how this results we can examine the
characteristics of the 1st and 3rd terms in the equalization transfer function with Fst = F1:
required equalization really is. Let us examine the equation term by term. The first two terms shift the
drivers poles to achieve a Q = 0.5 response at Fc and are recognized as 1st order shelving functions
with gains, G1 = F1/Fc, and G2 = F2/Fc. (Note that G1 < 1.0 and G2 > 1.0 if F1< Fc< F2.) The third
term is the gradient equalization which is also a shelving function with gain, Gst = Fp/Fst where Fst is
the frequency where the equalization is stopped. The center frequencies of the shelving filters are
given as sqrt(F1 x Fc), sqrt(F2 x Fc), and sqrt(Fp x Fst). The fourth term is a Q boost filter with gain,
Gd = Qd/ Qc and center frequency Fc, introduced to raise the response Q from Qc = 0.5 to the
desired Qd. The last term is a simple attenuation by 10 dB. Terms 1, 2 and 4 could be replaced by a
Linkwitz transformation if suitable. However, if the desired woofer target response is for Q = 0.5, term
4 is omitted and as to be shown, terms 1 and 3 can be combined into a single shelving function
making the equalization a simple combination of two shelving functions.
It was previously stated that if the woofer was low Q with F1 well below (an octave or more) the
desired cut off frequency then the gradient equalization could be curtailed at F1 yielding a
simplification in the equalization transfer function. To see how this results we can examine the
characteristics of the 1st and 3rd terms in the equalization transfer function with Fst = F1:

With the equalization curtailed at some frequency, Fst, a general transfer function for the complete
equalization of a gradient woofer system using a driver with Qts less than 0.5 can be expressed as:
equalization of a gradient woofer system using a driver with Qts less than 0.5 can be expressed as:

Thus, the 1st and 3rd terms can be combined into a single 1st order shelving response resulting in
the potential to achieve the required equalization with a circuit consisting of two shelving functions, a
Q boost circuit, if required, and 10dB attenuation.
2nd order high pass response:
As an example of this type of equalization consider a woofer with Qts = 0.2 and Fs = 18 Hz. F1 and
F2 are 3.8 and 86.2 Hz respectively. It is desired to equalize the response to Fc = 25 Hz, Q = 0.7 for
a gradient woofer system with an effective separation of 2 feet separation. Figure 3b shows the ideal,
unequalized on axis response in red and the equalized response in blue. Three stages of
equalization shown in Figure 3a are used, a shelf filter to shift the pole at F2 to Fc, a shelf filter which
is the combination of the gradient equalization and shifting the pole at F1 to Fc, and the Q boost filter
to obtain Q = 0.7 at Fc. As is apparent, the equalized response follows the Q = 0.7, 25 Hz target.
However, while not readily apparent in Figure 3b since F1 is at 3.8 Hz, ultimately the equalized
response will roll off at 3rd order due to the effective termination of the dipole equalization at F1.
the potential to achieve the required equalization with a circuit consisting of two shelving functions, a
Q boost circuit, if required, and 10dB attenuation.
2nd order high pass response:
As an example of this type of equalization consider a woofer with Qts = 0.2 and Fs = 18 Hz. F1 and
F2 are 3.8 and 86.2 Hz respectively. It is desired to equalize the response to Fc = 25 Hz, Q = 0.7 for
a gradient woofer system with an effective separation of 2 feet separation. Figure 3b shows the ideal,
unequalized on axis response in red and the equalized response in blue. Three stages of
equalization shown in Figure 3a are used, a shelf filter to shift the pole at F2 to Fc, a shelf filter which
is the combination of the gradient equalization and shifting the pole at F1 to Fc, and the Q boost filter
to obtain Q = 0.7 at Fc. As is apparent, the equalized response follows the Q = 0.7, 25 Hz target.
However, while not readily apparent in Figure 3b since F1 is at 3.8 Hz, ultimately the equalized
response will roll off at 3rd order due to the effective termination of the dipole equalization at F1.

While the equalization procedure described above provides the desired result it should be noted that
equalizing a 1st order gradient woofer response to a 2nd order high pass characteristic is not always
the good idea. The reason for this is straight forward. As is well known, for a sealed box woofer
system with 2nd order roll off the excursion below the cut off frequency becomes constant with
frequency for a given input level. However, for a gradient woofer equalized to a 2nd order high pass
response the excursion will continue to increase as 1/F below the cut off frequency. This means that
a gradient woofer is much more easily subjected to over excursion at low frequency, particularly
below the cut off frequency.
3rd order high pass response:
To minimize this risk a gradient woofer should have a minimum of a 3rd order high pass response.
One way to achieve this would be to add a 1st order low pass filter to the equalization above. For
example, the basic response could be equalized to a 2nd order, Q = 1.0 response and a 1st order
high pass filter at Fc added yielding a 3rd order Butterworth response. This result is shown in violet
in Figure 4.
equalizing a 1st order gradient woofer response to a 2nd order high pass characteristic is not always
the good idea. The reason for this is straight forward. As is well known, for a sealed box woofer
system with 2nd order roll off the excursion below the cut off frequency becomes constant with
frequency for a given input level. However, for a gradient woofer equalized to a 2nd order high pass
response the excursion will continue to increase as 1/F below the cut off frequency. This means that
a gradient woofer is much more easily subjected to over excursion at low frequency, particularly
below the cut off frequency.
3rd order high pass response:
To minimize this risk a gradient woofer should have a minimum of a 3rd order high pass response.
One way to achieve this would be to add a 1st order low pass filter to the equalization above. For
example, the basic response could be equalized to a 2nd order, Q = 1.0 response and a 1st order
high pass filter at Fc added yielding a 3rd order Butterworth response. This result is shown in violet
in Figure 4.

While this approach to achieving a 3rd order high pass response works, it is overly complicated and
required more active stages and components that required. A novel approach for achieving a 3rd
order high pass response with a low Q woofer is implemented using the simple equalization transfer
function below which schematic shown in Figure 5a:
required more active stages and components that required. A novel approach for achieving a 3rd
order high pass response with a low Q woofer is implemented using the simple equalization transfer
function below which schematic shown in Figure 5a:
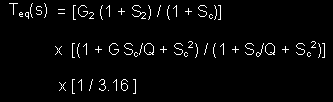
Here the 1st term is a shelving function used to shift the driver pole F2 to Fc as was used in the
previous case. The second term is a Q boost filter. However, here it is designed to provide both the
necessary correction to the woofer response and the equalization for the gradient roll off below Fp.
The gain, G, and Q of this stage are given as:
previous case. The second term is a Q boost filter. However, here it is designed to provide both the
necessary correction to the woofer response and the equalization for the gradient roll off below Fp.
The gain, G, and Q of this stage are given as:
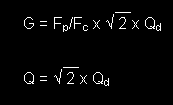
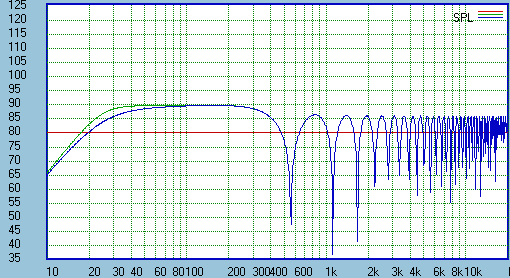
The response at Fc will be at 20 Log(Qd) dB. Thus for Qd = 0.7 the response will be down 3dB at
Fc and for Qd = 0.5 down 6dB. Such responses are shown in Figure 5b in green and blue,
respectively. This approach to equalization yields a very simple circuit and good protection from
over excursion of the driver.
Fc and for Qd = 0.5 down 6dB. Such responses are shown in Figure 5b in green and blue,
respectively. This approach to equalization yields a very simple circuit and good protection from
over excursion of the driver.
4th order high pass response:
If the shifting of the low frequency pole, F1, to Fc is retained in the equalization transfer function another
novel approach to equalization of a gradient woofer system can be obtained which yields a 4th order roll
off. In this case the equalization function is given as:
If the shifting of the low frequency pole, F1, to Fc is retained in the equalization transfer function another
novel approach to equalization of a gradient woofer system can be obtained which yields a 4th order roll
off. In this case the equalization function is given as:
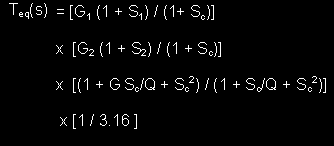
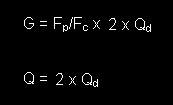
with the gain, G and the Q of the boost filter given as:
An example of this type of equalization is shown in Figure6 for Qd = 0.7 in green and 0.5 in blue. These
correspond to 4th order Butterworth and Linkwitz/Riley responses, respectively and yield further
protection form driver over excursion below Fc. Again, the response at Fc will be down 20 Log(Qd) dB
correspond to 4th order Butterworth and Linkwitz/Riley responses, respectively and yield further
protection form driver over excursion below Fc. Again, the response at Fc will be down 20 Log(Qd) dB
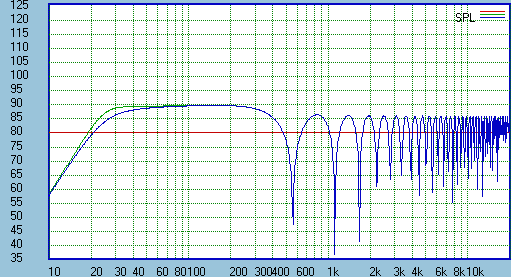
In conclusion what has been demonstrated is that the response of a gradient woofer system based on a
driver with Qts < 0.5 and for which the low frequency pole, F1, is well below the desired system cut off
frequency, Fc, can be equalized to the desired 2nd, 3rd or 4th order target response using simple
active circuit consisting of at most two 1st order shelving functions and a Q boost filter at Fc. When the
driver has Qts > 0.5 and Fs is acceptable as the system cut off frequency the equalization can be
accomplished using, at most, a single shelving filter and a Q boost filter.
driver with Qts < 0.5 and for which the low frequency pole, F1, is well below the desired system cut off
frequency, Fc, can be equalized to the desired 2nd, 3rd or 4th order target response using simple
active circuit consisting of at most two 1st order shelving functions and a Q boost filter at Fc. When the
driver has Qts > 0.5 and Fs is acceptable as the system cut off frequency the equalization can be
accomplished using, at most, a single shelving filter and a Q boost filter.
Figure 1
Figure 2
Figure 3a
Figure 4
Figure 5b
Figure 6b
Equalization for driver with Qts less than 0.5
Equalization for drivers with Qts greater than 0.5 and acceptable Fs
The previous discussion considered driver with Qts less then 0.5 and with poles at frequencies, F1
and F2 (Fs = sqrt(F1 x F2), spanning the expected low frequency cut off, Fc, of the woofer system. If
by chance a suitable woofer is selected which has Qts greater then 0.5 and Fs such that the system
Fc = the driver Fs then even greater simplicity in equalization is possible for 2nd order, 3rd order and
4th order high pass response. These will be discuss briefly below.
2nd order high pass equalization:
In this case all that is required is a single stage of equalization consisting of a 1st order shelving
function to compensate for the gradient roll off. The equalization transfer functions is of the form:
and F2 (Fs = sqrt(F1 x F2), spanning the expected low frequency cut off, Fc, of the woofer system. If
by chance a suitable woofer is selected which has Qts greater then 0.5 and Fs such that the system
Fc = the driver Fs then even greater simplicity in equalization is possible for 2nd order, 3rd order and
4th order high pass response. These will be discuss briefly below.
2nd order high pass equalization:
In this case all that is required is a single stage of equalization consisting of a 1st order shelving
function to compensate for the gradient roll off. The equalization transfer functions is of the form:

where Gst = Fp/Fst. Here Fst must be chosen to be at least an octave below Fc. Ulitmately the
response will roll off at 3rd order below Fst. The factor of 1/3.16 is the required 10dB attenuation.
The final response Q will be the same as that of the driver.
3rd order high pass equalization:
To obtain a 3rd order high pass response the equalization transfer function is the product 1st order
shelving and a Q boost filter, similar to that of the low Q driver:
response will roll off at 3rd order below Fst. The factor of 1/3.16 is the required 10dB attenuation.
The final response Q will be the same as that of the driver.
3rd order high pass equalization:
To obtain a 3rd order high pass response the equalization transfer function is the product 1st order
shelving and a Q boost filter, similar to that of the low Q driver:
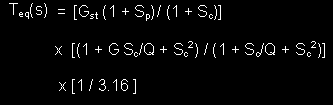
Here Gst = Fp/Fc = Fp/Fs but the gain, G and Q of the boost filter are defined some what differently
than for low Qts case. For a given driver Qts and a desired response Qd,
than for low Qts case. For a given driver Qts and a desired response Qd,
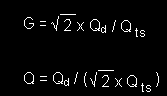
provided that Qd is greater than 0.5.
4th order high pass response:
Equalizing the response of a driver with Qts greater than 0.5 for a 4th order high pass response
requires an equalization transfer function which is just a simple Q boost filter. Recall that for a low Q
woofer the equalization consisted of two 1st order shelving filters to shift the driver poles to the
desired cut off frequency yielding a Q = 0.5 response which was then equalized to flat and the
desired Qd using a Q boost filter. When the driver already has Qts greater than 0.5 and the driver
Fs is acceptable as the system cut off, Fc the equalization transfer function becomes:
4th order high pass response:
Equalizing the response of a driver with Qts greater than 0.5 for a 4th order high pass response
requires an equalization transfer function which is just a simple Q boost filter. Recall that for a low Q
woofer the equalization consisted of two 1st order shelving filters to shift the driver poles to the
desired cut off frequency yielding a Q = 0.5 response which was then equalized to flat and the
desired Qd using a Q boost filter. When the driver already has Qts greater than 0.5 and the driver
Fs is acceptable as the system cut off, Fc the equalization transfer function becomes:
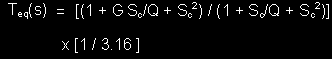
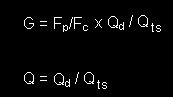
Where G and Q for the Q boost filter are given as:
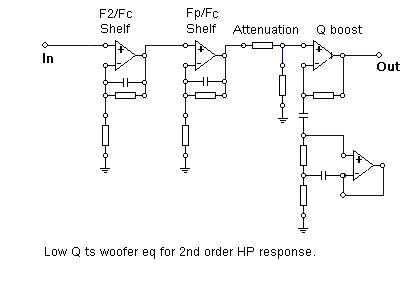
Figure 3b
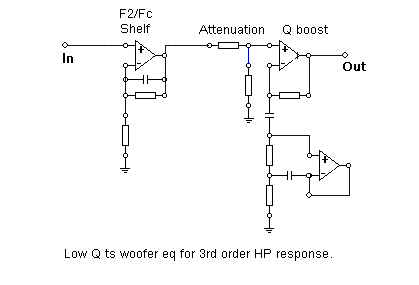
Figure 5a
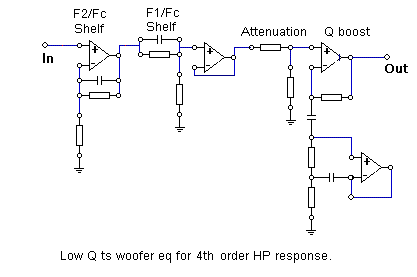
Figure 6a