Tech Design.....
___________________________
Power Matching woofers to midranges and satellite speakers.
___________________________
Power Matching woofers to midranges and satellite speakers.
When designing a full range speaker system or adding a woofer to a satellite system there are a number of factors
which should be considered. Among these are size, cost, efficiency, placement, maximum required sound
pressure, distortion, excitation of room modes, and total radiated acoustic power. Here we shall focus on this last
factor, total radiated acoustic power. One reasonable premise is that total radiated acoustic power by the speaker
system should be constant over as wide a frequency range as possibly. Indeed, this seems more than reasonable,
it seems as if dictated by common sense. However, just what does this imply about the characteristics of the
system with regard to directivity or radiation pattern? To begin we need to consider the directivity factor of a sound
source, DF(f), which is generally frequency and position dependent. For the purpose of this discussion it will be
acceptable to assume that DF is constant with frequency. Beranek [1] defines the DF as follows:
"The directivity factor is the ratio of the intensity on a designated axis of a sound radiator at a stated distance r to
the intensity that would be produced at the same position by a point source if it were radiating the same total
acoustic power as the radiator."
He continues,
"Free space is assumed for the measurements. Usually, the designated axis is taken as the axis of maximum
radiation."
The on axis, free space directivity factor for sound sources with several common free space radiation patterns are
as follows: Monopole, DF = 1.0, Dipole, DF = 3, Cardioid, DF = 3. What this means is that if these three different
sources are to radiate the same total acoustic power then if the monopole has an on axis intensity of 1.0 the dipole
and cardioid will have an on axis intensity of 3.0 or 4.77 dB greater. Conversely, if the difference sources are to
have the same on axis intensity then the dipole and cardioid will radiate 1/3 the acoustic power of the monopole.
(As an aside, for those familiar with room acoustics and reverberation this means that the critical distance from the speaker will be
greater for a dipole or cardioid than for a monopole. The critical distance is the distance at which direct and reflected sound are equal.
The level of the reflected sound, above the modal region of the room, is usually considered constant and proportional to the total
radiated power. Thus when sitting the same distance from a conventional speaker and a dipole, the dipole can potentially sound
more detailed since at the position that ratio of direct to reflected sound is greater for the dipole.) Clearly it would appear that if
DF is not frequency dependent then a speaker system would radiate constant power from which it would follow that
a monopole midrange or satellite speaker should be match with a monopole woofer, a dipole with a dipole and a
cardioid with a cardioid. Since cardioids and dipoles have the same DF it would also appear, form a power
perspective, that a dipole and a cardioid can also be matched.
Unfortunately things just aren't so simple. The above argument is keyed to one unmentioned factor, that the space
the source is radiating into is also frequency independent. Obviously, if the sources are in free space this is the
case. It would also be the case if the source were mounted in a true infinite baffle, or along the line of intersection
of to planes perpendicular to each other, or at the corner formed by three plane where are all mutually
perpendicular. These arrangements amount to what is commonly referred to as 4Pi, 2Pi, Pi, and Pi/2 space.
We are all familiar with the transition between 4Pi and 2Pi space know as the baffle step. We know that as the
transition occurs the on axis sound pressure increases by 6dB. But what about radiated power? Consider for the
moment a sealed box woofer operating at low frequency such that in free space the radiation is that of a
monopole. This corresponds to a driver radiating in the center of a sphere, as shown in Figure 1. The radiated
power is the integral of the intensity, I, over the surface of the sphere enclosing the source. If we let the radius,r,
equal 1.0 and the intensity equal 1.0, the radiated power for the monopole would be 4Pi. If the source were a
which should be considered. Among these are size, cost, efficiency, placement, maximum required sound
pressure, distortion, excitation of room modes, and total radiated acoustic power. Here we shall focus on this last
factor, total radiated acoustic power. One reasonable premise is that total radiated acoustic power by the speaker
system should be constant over as wide a frequency range as possibly. Indeed, this seems more than reasonable,
it seems as if dictated by common sense. However, just what does this imply about the characteristics of the
system with regard to directivity or radiation pattern? To begin we need to consider the directivity factor of a sound
source, DF(f), which is generally frequency and position dependent. For the purpose of this discussion it will be
acceptable to assume that DF is constant with frequency. Beranek [1] defines the DF as follows:
"The directivity factor is the ratio of the intensity on a designated axis of a sound radiator at a stated distance r to
the intensity that would be produced at the same position by a point source if it were radiating the same total
acoustic power as the radiator."
He continues,
"Free space is assumed for the measurements. Usually, the designated axis is taken as the axis of maximum
radiation."
The on axis, free space directivity factor for sound sources with several common free space radiation patterns are
as follows: Monopole, DF = 1.0, Dipole, DF = 3, Cardioid, DF = 3. What this means is that if these three different
sources are to radiate the same total acoustic power then if the monopole has an on axis intensity of 1.0 the dipole
and cardioid will have an on axis intensity of 3.0 or 4.77 dB greater. Conversely, if the difference sources are to
have the same on axis intensity then the dipole and cardioid will radiate 1/3 the acoustic power of the monopole.
(As an aside, for those familiar with room acoustics and reverberation this means that the critical distance from the speaker will be
greater for a dipole or cardioid than for a monopole. The critical distance is the distance at which direct and reflected sound are equal.
The level of the reflected sound, above the modal region of the room, is usually considered constant and proportional to the total
radiated power. Thus when sitting the same distance from a conventional speaker and a dipole, the dipole can potentially sound
more detailed since at the position that ratio of direct to reflected sound is greater for the dipole.) Clearly it would appear that if
DF is not frequency dependent then a speaker system would radiate constant power from which it would follow that
a monopole midrange or satellite speaker should be match with a monopole woofer, a dipole with a dipole and a
cardioid with a cardioid. Since cardioids and dipoles have the same DF it would also appear, form a power
perspective, that a dipole and a cardioid can also be matched.
Unfortunately things just aren't so simple. The above argument is keyed to one unmentioned factor, that the space
the source is radiating into is also frequency independent. Obviously, if the sources are in free space this is the
case. It would also be the case if the source were mounted in a true infinite baffle, or along the line of intersection
of to planes perpendicular to each other, or at the corner formed by three plane where are all mutually
perpendicular. These arrangements amount to what is commonly referred to as 4Pi, 2Pi, Pi, and Pi/2 space.
We are all familiar with the transition between 4Pi and 2Pi space know as the baffle step. We know that as the
transition occurs the on axis sound pressure increases by 6dB. But what about radiated power? Consider for the
moment a sealed box woofer operating at low frequency such that in free space the radiation is that of a
monopole. This corresponds to a driver radiating in the center of a sphere, as shown in Figure 1. The radiated
power is the integral of the intensity, I, over the surface of the sphere enclosing the source. If we let the radius,r,
equal 1.0 and the intensity equal 1.0, the radiated power for the monopole would be 4Pi. If the source were a
dipole or cardioid the total radiated power would be 4Pi/3,
or in general, 4PI/DF. Now consider the same source
placed at the origin of the hemisphere shown in Figure 2.
For a source other than a monopole let the axis of the
source lay in the X-Z plane dividing the sphere into a
or in general, 4PI/DF. Now consider the same source
placed at the origin of the hemisphere shown in Figure 2.
For a source other than a monopole let the axis of the
source lay in the X-Z plane dividing the sphere into a

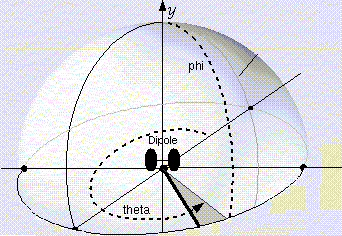
Figure 2. 2 Pi space. The sound source is at
the origin.
the origin.
Figure 1. 4 Pi space. The sound source is at
the origin.
the origin.
hemisphere and assume that the radiation pattern is symmetric about the axis of the source. Further assume
that the same electrical power is input to the source. Since the same electrical signal is forcing the motion of
the driver the motion will remain the same. The motion of the driver will therefore displace the same volume of
air as it moves. However, this volume of air is now required to move though only 1/2 the area, the upper
surface area of the hemisphere. Conservation of mass requires that the velocity of the air passing through the
surface is equal to the volume flow of the air divided by the surface area. Since the volume of air displace by
the driver remains constant the velocity must double when the area is cut in half. The sound pressure is given
by the product of the velocity at the surface of the sphere times the specific acoustic impedance[1].
Therefore, if the velocity doubles so will the sound pressure. The intensity, I, is proportional to the sound
pressure squared. So the intensity increases by a factor of 4. Finally, the total radiated power is the integral of
the intensity over the surface area of the hemisphere or, P = 4 x 2PI/DF = 8 Pi /DF. This is twice (+3dB) the
total power radiated by the same source when radiating into 4Pi space and the doubling of the sound
pressure corresponds to a 6dB increase in sound pressure level. This is a well known result and shows that
not only does the sound pressure level increase by 6dB but also that the efficiency of a sound source doubles
when operating in a 2Pi environment [2].
Now we ask, what happens if the signal to the driver is adjusted so that the on axis intensity and sound
pressure are the same as when the driver is radiating into 4Pi space? This requires that the sound pressure
be reduced to 1.0 which in turn reduces the intensity back to 1.0 in which case the total radiated power into
2Pi space will be 2Pi/DF. This is -3dB relative to a source with the same DF radiating at the same on axis level
in to 4Pi space. The physics is quite simple. The intensity is constant but the area over which it radiates is
reduced by 1/2 when radiating into 2Pi space so the total power is also reduced by 1/2.
The important conclusion is that when a source with a given DF is radiating into 2Pi space it will
radiate 3dB less total acoustic power than when radiating in to 4Pi space provided the on axis
intensity or sound pressure level are identical.
This is an interesting observation but you may be asking what this has to do with integrating a woofer system
with a midrange driver or a satellite speaker system when considering uniformity of the radiated power
response? The missing element is a function describing how the radiation space varies with frequency and
placement of the sources. If we consider a single source positioned at some distance above a ground plane
(GP) or floor, and we consider only the effect of the floor, the effective space into which it radiates will
undergo a transition from 4Pi to 2Pi as the wave length of the radiated sound becomes long relative
to the distance between the source and the GP. It follows from the conclusion presented above that, if the
source has constant DF and is designed to radiate flat on axis frequency response it must
necessarily radiate 3dB less acoustic power at low frequency than it does at high frequency. This is
shown pictorially in Figure 3, to the left. Thus the supposition that a speaker system with constant directivity
and flat frequency response will radiate constant power at all frequencies is not correct unless the space into
which the speaker radiates is constant. This will not be the case unless the speaker has limited low frequency
extension such that the lowest frequency radiated has a wave length less than the distance to a boundary
(floor, wall ceiling, etc). This may be the case for satellite speakers mounted on stands, or for in wall speakers
where the distance to an adjacent wall, the ceiling or floor is greater than the wave length of the lowest
frequency the system produces.
However, if we consider a typically floor standing 3-way speaker system it would not be unusual to find the
woofer located close to the floor and the midrange at a height of 2 to 3 feet above the floor. If we further
assume that other than the floor the speaker is positioned far from other surfaces then we can see that
somewhere across the frequency range of the system a transition form 4PI to 2Pi radiation will occur.
Furthermore, since the woofer and midrange are at different distances from the floor this GP related transition
can occur at different frequencies for different drivers. If we assume that the wave length is long compared to
the distance between the source and the GP when the wave length is 3 times that distance, then a midrange
driver positioned 3 feet from the floor would be operating in a 4Pi environment above approximately 125 Hz
(wave length 9 feet). This is a reasonable lower limit for the crossover point of a midrange driver. Thus we
may consider the midrange to operate in 4Pi space and have uniform radiated total power as long as its DF
remains constant (and we are below the baffle step frequency for a monopole system). By the same
arguments, the woofer system, being close to the floor, say 1 foot above the GP, will be operating in 2Pi
space at frequencies as high as 375 Hz. Thus the woofer can be considered to operate in 2Pi space over its
entire frequency range. Now, returning to the conclusion reached above we can see that if the midrange and
the woofer have the same DF and the system is designed to have flat on axis response over its entire
frequency range, then the total acoustic power radiated by the woofer will be 3dB below the power
radiated by the midrange. This result is independent of the system type, be it a full range monopole,
dipole or cardioid.
Since it has been shown that a speaker system with constant directivity is not the solution to
constant total radiated power we can ask ourselves what can be done to realize the constant power
solution, at least if we restrict the argument to the presence of a ground plane. One potential solution would
be using sources with different DF. For example, with a 3-way system of the format above if the midrange
were a dipole or cardioid the radiated power would be 4Pi/3. Since the woofer is operating in 2Pi space its
radiated power would be 2Pi/DFw where the subscript indicates the DF of the woofer. If DFw = 1.5 then the
woofer would radiate the same total acoustic power as the midrange when both had the same on axis intensity.
Before discussing how such a woofer could be constructed it is instructive to considerer what the result
would be if a speaker with a dipole midrange were mated with a monopole woofer system.
In this case the midrange would still radiate a power of 4Pi/3, but the woofer would radiate a power of 2Pi
when the on axis response is matched to the midrange level. This results in the woofer radiating 1.5 time the
power or +1.76dB more power than the midrange. While not a perfect match, it is certainly better than the
-3dB result obtained by using a dipole or cardioid woofer system, or by using a monopole midrange with a
monopole woofer.
So how can this power mismatch be corrected? That depends on the type of speaker system. If we look
at the case of a monopole midrange there is a fairly easy solution. Such a system will typically already have a
4Pi to 2Pi transition at higher frequency dictated by the baffle step. Thus, all that need be done is to make the
baffle sufficiently large that the baffle step is below the low frequency cut off of the midrange. In this case the
midrange will radiate constant power into 2Pi space as long as its DF remains close to 1, i.e. below the
frequency at which the midrange driver becomes directional. Both the monopole woofer and the midrange will
radiate the same acoustic power when the on axis response is flat. While a potential solution, it is in conflict
with the current trends of narrow baffles. We should also note that a monopole midrange radiating into
2Pi space radiates only 1.76 dB more total power than a dipole midrange radiating into 4Pi space,
the typical dipole midrange format. Perhaps the trend towards narrow baffles is actually a step backwards for
conventional speakers?
If we consider a speaker with a dipole or cardioid midrange response there are a number of
potential solutions. Considering a dipole system first, if we restrict ourselves to a dipole woofer with its axis
aligned with the midrange then the only way to match the midrange power is to double the on axis intensity of
the woofer. Unfortunately this corresponds to a 3dB increase in the on axis sound pressure level. However,
recall form the definition of DF that it is usually defined on the axis of maximum radiation. For a dipole DF will
vary as we move off axis from the maximum of 3 on axis to 0 at 90 degrees off axis. At 45 degrees DF for a
dipole is 1.5. Thus if the woofer system is rotated such that the woofer axis is at 45 degrees relative to the axis
of the midrange, which we shall take as the axis of the speaker system, the response of the woofer on the
system axis would match that of the midrange when it is radiating the same total acoustic power. With a stereo
pair of woofers rotated inward towards the listening position such an arrangement could potentially yield a
more uniform low frequency sound field to the left and right of the listening position since as the listener
moved to the left the drop off of the left woofer, due to the dipole polar response would be compensated for
by the increase on the output from the right side woofer. Such an arrangement is shown in Figure 4. The
dipole woofers are rotated 45 degrees relative to the speaker (and midrange) axis. The green lines show the
increased bass level radiated form the left woofer could potentially compensate for the drop
that the same electrical power is input to the source. Since the same electrical signal is forcing the motion of
the driver the motion will remain the same. The motion of the driver will therefore displace the same volume of
air as it moves. However, this volume of air is now required to move though only 1/2 the area, the upper
surface area of the hemisphere. Conservation of mass requires that the velocity of the air passing through the
surface is equal to the volume flow of the air divided by the surface area. Since the volume of air displace by
the driver remains constant the velocity must double when the area is cut in half. The sound pressure is given
by the product of the velocity at the surface of the sphere times the specific acoustic impedance[1].
Therefore, if the velocity doubles so will the sound pressure. The intensity, I, is proportional to the sound
pressure squared. So the intensity increases by a factor of 4. Finally, the total radiated power is the integral of
the intensity over the surface area of the hemisphere or, P = 4 x 2PI/DF = 8 Pi /DF. This is twice (+3dB) the
total power radiated by the same source when radiating into 4Pi space and the doubling of the sound
pressure corresponds to a 6dB increase in sound pressure level. This is a well known result and shows that
not only does the sound pressure level increase by 6dB but also that the efficiency of a sound source doubles
when operating in a 2Pi environment [2].
Now we ask, what happens if the signal to the driver is adjusted so that the on axis intensity and sound
pressure are the same as when the driver is radiating into 4Pi space? This requires that the sound pressure
be reduced to 1.0 which in turn reduces the intensity back to 1.0 in which case the total radiated power into
2Pi space will be 2Pi/DF. This is -3dB relative to a source with the same DF radiating at the same on axis level
in to 4Pi space. The physics is quite simple. The intensity is constant but the area over which it radiates is
reduced by 1/2 when radiating into 2Pi space so the total power is also reduced by 1/2.
The important conclusion is that when a source with a given DF is radiating into 2Pi space it will
radiate 3dB less total acoustic power than when radiating in to 4Pi space provided the on axis
intensity or sound pressure level are identical.
This is an interesting observation but you may be asking what this has to do with integrating a woofer system
with a midrange driver or a satellite speaker system when considering uniformity of the radiated power
response? The missing element is a function describing how the radiation space varies with frequency and
placement of the sources. If we consider a single source positioned at some distance above a ground plane
(GP) or floor, and we consider only the effect of the floor, the effective space into which it radiates will
undergo a transition from 4Pi to 2Pi as the wave length of the radiated sound becomes long relative
to the distance between the source and the GP. It follows from the conclusion presented above that, if the
source has constant DF and is designed to radiate flat on axis frequency response it must
necessarily radiate 3dB less acoustic power at low frequency than it does at high frequency. This is
shown pictorially in Figure 3, to the left. Thus the supposition that a speaker system with constant directivity
and flat frequency response will radiate constant power at all frequencies is not correct unless the space into
which the speaker radiates is constant. This will not be the case unless the speaker has limited low frequency
extension such that the lowest frequency radiated has a wave length less than the distance to a boundary
(floor, wall ceiling, etc). This may be the case for satellite speakers mounted on stands, or for in wall speakers
where the distance to an adjacent wall, the ceiling or floor is greater than the wave length of the lowest
frequency the system produces.
However, if we consider a typically floor standing 3-way speaker system it would not be unusual to find the
woofer located close to the floor and the midrange at a height of 2 to 3 feet above the floor. If we further
assume that other than the floor the speaker is positioned far from other surfaces then we can see that
somewhere across the frequency range of the system a transition form 4PI to 2Pi radiation will occur.
Furthermore, since the woofer and midrange are at different distances from the floor this GP related transition
can occur at different frequencies for different drivers. If we assume that the wave length is long compared to
the distance between the source and the GP when the wave length is 3 times that distance, then a midrange
driver positioned 3 feet from the floor would be operating in a 4Pi environment above approximately 125 Hz
(wave length 9 feet). This is a reasonable lower limit for the crossover point of a midrange driver. Thus we
may consider the midrange to operate in 4Pi space and have uniform radiated total power as long as its DF
remains constant (and we are below the baffle step frequency for a monopole system). By the same
arguments, the woofer system, being close to the floor, say 1 foot above the GP, will be operating in 2Pi
space at frequencies as high as 375 Hz. Thus the woofer can be considered to operate in 2Pi space over its
entire frequency range. Now, returning to the conclusion reached above we can see that if the midrange and
the woofer have the same DF and the system is designed to have flat on axis response over its entire
frequency range, then the total acoustic power radiated by the woofer will be 3dB below the power
radiated by the midrange. This result is independent of the system type, be it a full range monopole,
dipole or cardioid.
Since it has been shown that a speaker system with constant directivity is not the solution to
constant total radiated power we can ask ourselves what can be done to realize the constant power
solution, at least if we restrict the argument to the presence of a ground plane. One potential solution would
be using sources with different DF. For example, with a 3-way system of the format above if the midrange
were a dipole or cardioid the radiated power would be 4Pi/3. Since the woofer is operating in 2Pi space its
radiated power would be 2Pi/DFw where the subscript indicates the DF of the woofer. If DFw = 1.5 then the
woofer would radiate the same total acoustic power as the midrange when both had the same on axis intensity.
Before discussing how such a woofer could be constructed it is instructive to considerer what the result
would be if a speaker with a dipole midrange were mated with a monopole woofer system.
In this case the midrange would still radiate a power of 4Pi/3, but the woofer would radiate a power of 2Pi
when the on axis response is matched to the midrange level. This results in the woofer radiating 1.5 time the
power or +1.76dB more power than the midrange. While not a perfect match, it is certainly better than the
-3dB result obtained by using a dipole or cardioid woofer system, or by using a monopole midrange with a
monopole woofer.
So how can this power mismatch be corrected? That depends on the type of speaker system. If we look
at the case of a monopole midrange there is a fairly easy solution. Such a system will typically already have a
4Pi to 2Pi transition at higher frequency dictated by the baffle step. Thus, all that need be done is to make the
baffle sufficiently large that the baffle step is below the low frequency cut off of the midrange. In this case the
midrange will radiate constant power into 2Pi space as long as its DF remains close to 1, i.e. below the
frequency at which the midrange driver becomes directional. Both the monopole woofer and the midrange will
radiate the same acoustic power when the on axis response is flat. While a potential solution, it is in conflict
with the current trends of narrow baffles. We should also note that a monopole midrange radiating into
2Pi space radiates only 1.76 dB more total power than a dipole midrange radiating into 4Pi space,
the typical dipole midrange format. Perhaps the trend towards narrow baffles is actually a step backwards for
conventional speakers?
If we consider a speaker with a dipole or cardioid midrange response there are a number of
potential solutions. Considering a dipole system first, if we restrict ourselves to a dipole woofer with its axis
aligned with the midrange then the only way to match the midrange power is to double the on axis intensity of
the woofer. Unfortunately this corresponds to a 3dB increase in the on axis sound pressure level. However,
recall form the definition of DF that it is usually defined on the axis of maximum radiation. For a dipole DF will
vary as we move off axis from the maximum of 3 on axis to 0 at 90 degrees off axis. At 45 degrees DF for a
dipole is 1.5. Thus if the woofer system is rotated such that the woofer axis is at 45 degrees relative to the axis
of the midrange, which we shall take as the axis of the speaker system, the response of the woofer on the
system axis would match that of the midrange when it is radiating the same total acoustic power. With a stereo
pair of woofers rotated inward towards the listening position such an arrangement could potentially yield a
more uniform low frequency sound field to the left and right of the listening position since as the listener
moved to the left the drop off of the left woofer, due to the dipole polar response would be compensated for
by the increase on the output from the right side woofer. Such an arrangement is shown in Figure 4. The
dipole woofers are rotated 45 degrees relative to the speaker (and midrange) axis. The green lines show the
increased bass level radiated form the left woofer could potentially compensate for the drop

Figure 3. Variation of radiated power
with frequency for a constant
directivity source with flat on axis
frequency response as it undergoes a
transition between a 4PI and 2Pi
environment due to the proximity to a
ground plane.
with frequency for a constant
directivity source with flat on axis
frequency response as it undergoes a
transition between a 4PI and 2Pi
environment due to the proximity to a
ground plane.
off of the right woofer. However, with
the speakers canted in towards the
listening position by 30 degrees, as
is typical, the dipole woofer is
rotated 75 degrees relative to the
front to back axis of the listening
room. And of course, there would be
complications with the crossover
from midrange to woofer in addition
to very different stimulation of room
modes. All in all a novel solution that
requires considerable more
investigation. (Note, such an
arrangement could also be
experimented with for midrange
reproduction.)
In the case of a cardioid woofer
system, a similar arrangement could
be made, however the rotation of the
woofers would have to be greater
since the DF = 1.5 point a cardioid is
close to 70 degrees off axis [3].
the speakers canted in towards the
listening position by 30 degrees, as
is typical, the dipole woofer is
rotated 75 degrees relative to the
front to back axis of the listening
room. And of course, there would be
complications with the crossover
from midrange to woofer in addition
to very different stimulation of room
modes. All in all a novel solution that
requires considerable more
investigation. (Note, such an
arrangement could also be
experimented with for midrange
reproduction.)
In the case of a cardioid woofer
system, a similar arrangement could
be made, however the rotation of the
woofers would have to be greater
since the DF = 1.5 point a cardioid is
close to 70 degrees off axis [3].
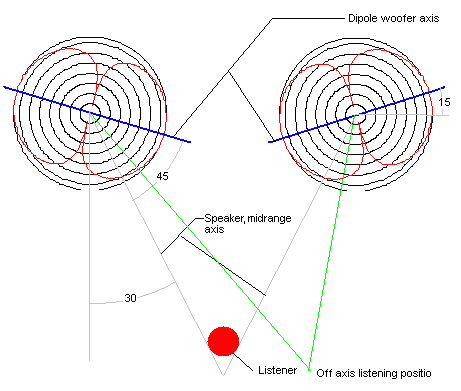
Figure 4. Novel positing of dipole woofer in a dipole system to
yield flat on axis response and flat power response.
yield flat on axis response and flat power response.

In view of the somewhat bizarre nature of these solutions to the power
response problem it is reasonable to look for a more appealing solution
where the axis of the woofer system is aligned with the axis of the
speaker. For this to be the case we must develop a woofer system with
an on axis, free space DF = 1.5. This can be accomplished by combining a
dipole woofer with a monopole. If we start with a dipole woofer and being to
sum its response to that of a monopole we find a gradual deformation of
the dipole radiation pattern into a cardioid at the point where the isolated
dipole and monopole on axis sound pressures are equal. Since the
cardioid still has a DF = 3, as for the dipole, it is unlikely that any of the
intermediate polar response patterns would result in our target DF = 1.5.
However, if we continue to increase the monopole strength above that of
the dipole the null to the rear of the cardioid begins to fill in. As the strength
of the monopole continues to increase relative to the dipole, the polar
pattern becomes that of a monopole with DF = 1. This variation in polar
response is shown in Figure 5. Clearly, somewhere between the cardioid
and the monopole there exists a situation where the relative strength of the
monopole and dipole are such that DF = 1.5 can be obtained on axis. Such
a polar pattern would be the desired response to achieve constant radiated
power between a dipole midrange operating in fee space, 4Pi, and a
woofer system operating in 2Pi space, as when the woofer is positioned
close to a ground plane. Further details of the design of a woofer system
with various DF can be found here.
response problem it is reasonable to look for a more appealing solution
where the axis of the woofer system is aligned with the axis of the
speaker. For this to be the case we must develop a woofer system with
an on axis, free space DF = 1.5. This can be accomplished by combining a
dipole woofer with a monopole. If we start with a dipole woofer and being to
sum its response to that of a monopole we find a gradual deformation of
the dipole radiation pattern into a cardioid at the point where the isolated
dipole and monopole on axis sound pressures are equal. Since the
cardioid still has a DF = 3, as for the dipole, it is unlikely that any of the
intermediate polar response patterns would result in our target DF = 1.5.
However, if we continue to increase the monopole strength above that of
the dipole the null to the rear of the cardioid begins to fill in. As the strength
of the monopole continues to increase relative to the dipole, the polar
pattern becomes that of a monopole with DF = 1. This variation in polar
response is shown in Figure 5. Clearly, somewhere between the cardioid
and the monopole there exists a situation where the relative strength of the
monopole and dipole are such that DF = 1.5 can be obtained on axis. Such
a polar pattern would be the desired response to achieve constant radiated
power between a dipole midrange operating in fee space, 4Pi, and a
woofer system operating in 2Pi space, as when the woofer is positioned
close to a ground plane. Further details of the design of a woofer system
with various DF can be found here.
Figure 5 Transition from dipole
to cardioid to monopole.
to cardioid to monopole.
In conclusion it has been shown that constant directionality, or uniformity in the polar response pattern does
not result in uniform power unless the sound source in question is restricted to radiating into a uniform
space as well. While this may be the case for a limited bandwidth system mounted on stands or in walls, the
restriction of uniform space will typically be violated for larger, full range speaker systems regardless of type.
The discussion has shown that for a typical speaker system with woofer close to the floor and midrange 2 to
3 feet above the floor, the woofer system should have a free space directivity factor, measured on axis, that
is 1/2 that of the midrange if constant radiated power with frequency is desired, assuming the midrange is
operating in 4Pi space. This result is independent of the midrange type, monopole, dipole or cardioid. For a
monopole speaker it was shown that this problem can be rectified by using a wide baffle, placing the baffle step
below the crossover point, so that the midrange driver is operating in 2Pi space over its entire frequency range.
It was also shown that for systems using conventional formats mating a dipole midrange with a monopole woofer
will yield more uniform power response than when using a dipole woofer. Finally, it was shown that for constant
power a woofer system to be mated to a dipole midrange should have a polar response lying somewhere
between that of a cardioid and that of a monopole to achieve the required directionality factor of 1.5. The
discussion has been limited to that of constant radiated power. Other factors which will impact system
performance, such as room modes, room pressurization below the room fundamental and crossover between
different sources have been neglected. These topics are addressed in other discussions (see the Tech menu).
____________________
References:
1. Beranek, L. L., Acoustics, McGraw Hill Book Company, NY, 1954.
2. D'Appolito, J., Testing Loudspeakers, Audio Amateur Press, Peterborough, NH, 1998.
3. Olson, H.F., Gradient Loudspeakers, JAES, March, 1973. Also, Loudspeakers an Anthology, Vol. 1, 1980.
not result in uniform power unless the sound source in question is restricted to radiating into a uniform
space as well. While this may be the case for a limited bandwidth system mounted on stands or in walls, the
restriction of uniform space will typically be violated for larger, full range speaker systems regardless of type.
The discussion has shown that for a typical speaker system with woofer close to the floor and midrange 2 to
3 feet above the floor, the woofer system should have a free space directivity factor, measured on axis, that
is 1/2 that of the midrange if constant radiated power with frequency is desired, assuming the midrange is
operating in 4Pi space. This result is independent of the midrange type, monopole, dipole or cardioid. For a
monopole speaker it was shown that this problem can be rectified by using a wide baffle, placing the baffle step
below the crossover point, so that the midrange driver is operating in 2Pi space over its entire frequency range.
It was also shown that for systems using conventional formats mating a dipole midrange with a monopole woofer
will yield more uniform power response than when using a dipole woofer. Finally, it was shown that for constant
power a woofer system to be mated to a dipole midrange should have a polar response lying somewhere
between that of a cardioid and that of a monopole to achieve the required directionality factor of 1.5. The
discussion has been limited to that of constant radiated power. Other factors which will impact system
performance, such as room modes, room pressurization below the room fundamental and crossover between
different sources have been neglected. These topics are addressed in other discussions (see the Tech menu).
____________________
References:
1. Beranek, L. L., Acoustics, McGraw Hill Book Company, NY, 1954.
2. D'Appolito, J., Testing Loudspeakers, Audio Amateur Press, Peterborough, NH, 1998.
3. Olson, H.F., Gradient Loudspeakers, JAES, March, 1973. Also, Loudspeakers an Anthology, Vol. 1, 1980.